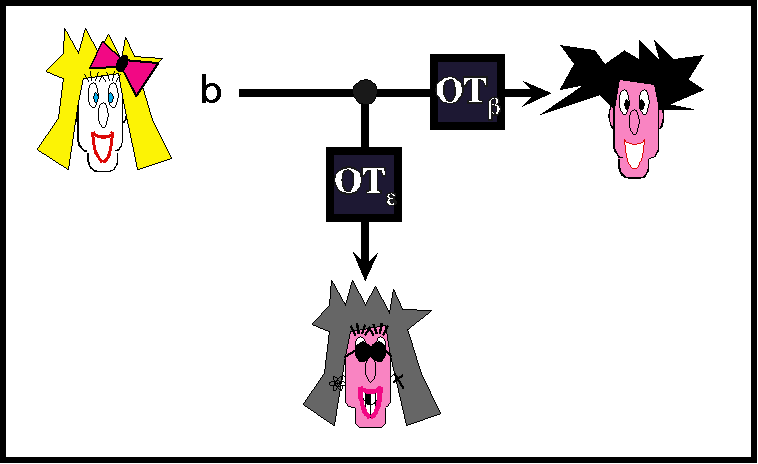
to evaluate secretly any two-party computation on private input A and B respectively. Don’t repeat everything we have done but use the things we have done and fill in the gaps.
EXTRA POINTS: when solving this question, make sure one party has all his data statistically concealed (whereas the other one is only computationally concealed).
Consider the standard basis S made of  and
and 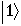 . We know that any pure state of a qubit can be expressed as a
. We know that any pure state of a qubit can be expressed as a +b
+b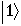 where a and b are complex numbers such that ||a||2+||b||2 = 1. Thus any element is specified by a pair (a,b) so that
where a and b are complex numbers such that ||a||2+||b||2 = 1. Thus any element is specified by a pair (a,b) so that  corresponds to (1,0) and
corresponds to (1,0) and 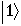 to (1,0). We have also seen that the diagonal basis D made of
to (1,0). We have also seen that the diagonal basis D made of 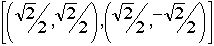 is conjugate to the standard basis which means that if we measure
is conjugate to the standard basis which means that if we measure  or
or 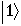 according to basis D the probabilities of each outcome are exactly 1/2.
according to basis D the probabilities of each outcome are exactly 1/2.
- Find yet a third basis C that is conjugate to both bases S and D.
- Find a basis B=[(u,v),(x,y)] such that measuring according to B maximizes the prediction probability for elements of bases S,D,C. More precisely, find a basis and a strategy that will have the highest success probability of issuing the correct answer when a random element of either S,D or C is given and that the basis is revealed after the measurement has been done.